1.图的表示

　　要表示一个图G=(V,E）,有两种标准方案，即零接表和零接矩阵。这两种表示法既可以用于有向图，也可以用于无向图。

2.广度优先搜索算法

　　在给定图G=(V,E),和一个特定的源定点s的情况下，广度优先搜索系统地搜索G中的边，以发现可以从s到达的顶点，并计算s到所有这些可以到达顶点之间的距离（即最少的边数）。该算法同时还能生成一棵根为s、且包括所有s的可以到达顶点的广度优先树。对从s可达的任意顶点v，广度优先树从s到v的路径对应于图G中从s到v的一条最短路径，及包含最少边的路径。

　　算法首先会发现和s距离为k的所有顶点，然后才会发现和s距离为K+1的其他顶点。广度优先算法将每个顶点着色为白色、灰色会黑色。

　　如下是BFS一个例子：

　　广度优先算法的运行时间是图G的邻接表大小的一个线程函数，BFS的总运行时间为O(V+E)。

广度优先树

　　BFS在搜索图的同时，也建立了一棵广度优先树，这棵树是由每个顶点中的π域所表示的。下面的过程将输出从s到v的最短路径上的所有顶点。

3.深度优先算法

　　深度优先算法的先辈子图形成了一个由数棵深度优先树所组成的深度优先森林。

　　下图说明了DFS的执行过程。

　　边的分类根据在图G上进行深度优先搜索所产生的深度优先森林Gπ，可以把图的边分为四张类型：

• 树边。是深度优先森林中，连接顶点V是在探寻边（u，v）时首次发现的，那么（u,v）就是一条树边。
• 反向边。是深度优先树中，连接顶点u到它的某一祖先顶点v的那些边。有向图中可能出现的自环也被认为是反向边。
• 正向边是指深度优先树中，连接顶点u到它的某个后裔v的非树边（u，v）。
• 交叉边是其他类型的边，存在于同一棵深度优先树的两个顶点之间，条件是其中一个顶点不是另一个顶点的祖先。交叉边也可以在不同的深度优先树的顶点之间。

拓扑排序

　　在许多应用中，有向无回路图用于说明事情发生的先后顺序。

 

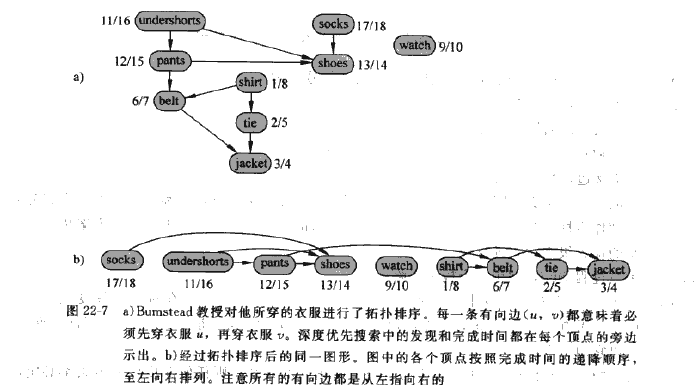
强连通分支

　　强连通（Strongly Connected）是指一个有向图（Directed Graph）中任意两点v1、v2间存在v1到v2的路径（path）及v2到v1的路径。